3000 Years of Algorithmic Rituals: The Emergence of AI from the Computation of Space
On AI as a long historical process of crystallizing collective behavior, personal data, and individual labor into privatized algorithms
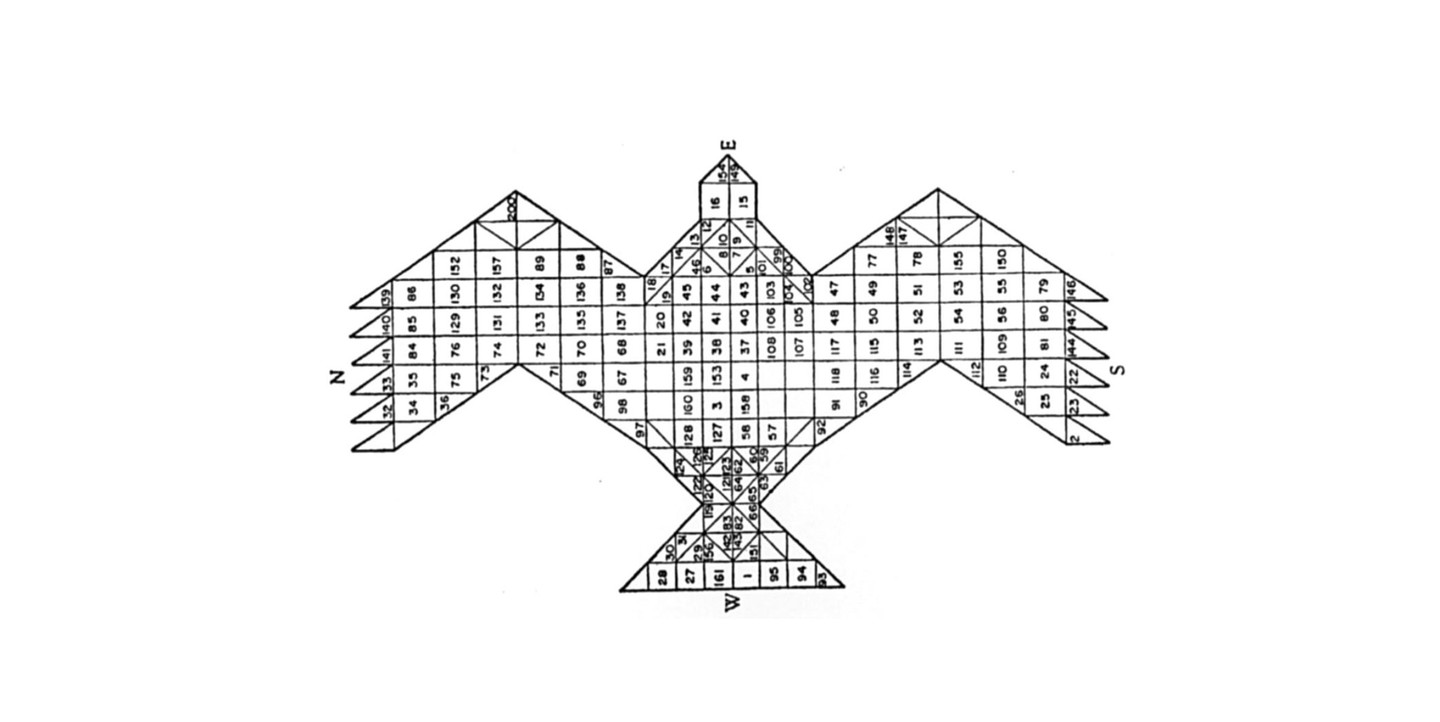
Image credit: Illustration from Frits Staal, "Greek and Vedic geometry" Journal of Indian Philosophy 27.1 (1999)
The following opinion piece originally appeared on Journal #101 of e-flux, and has been replicated here with the author’s permission.
With topographical memory, one could speak of generations of vision and even of visual heredity from one generation to the next. The advent of the logistics of perception and its renewed vectors for delocalizing geometrical optics, on the contrary, ushered in a eugenics of sight, a pre-emptive abortion of the diversity of mental images, of the swarm of image-beings doomed to remain unborn, no longer to see the light of day anywhere. —Paul Virilio, The Vision Machine1
1. Recomposing a Dismembered God
In a fascinating myth of cosmogenesis from the ancient Vedas, it is said that the god Prajapati was shattered into pieces by the act of creating the universe. After the birth of the world, the supreme god is found dismembered, undone. In the corresponding Agnicayana ritual, Hindu devotees symbolically recompose the fragmented body of the god by building a fire altar according to an elaborate geometric plan.2 The fire altar is laid down by aligning thousands of bricks of precise shape and size to create the profile of a falcon. Each brick is numbered and placed while reciting its dedicated mantra, following step-by-step instructions. Each layer of the altar is built on top of the previous one, conforming to the same area and shape. Solving a logical riddle that is the key of the ritual, each layer must keep the same shape and area of the contiguous ones, but using a different configuration of bricks. Finally, the falcon altar must face east, a prelude to the symbolic flight of the reconstructed god towards the rising sun—an example of divine reincarnation by geometric means.
The Agnicayana ritual is described in the Shulba Sutras, composed around 800 BCE in India to record a much older oral tradition. The Shulba Sutras teach the construction of altars of specific geometric forms to secure gifts from the gods: for instance, they suggest that “those who wish to destroy existing and future enemies should construct a fire-altar in the form of a rhombus.” 3 The complex falcon shape of the Agnicayana evolved gradually from a schematic composition of only seven squares. In the Vedic tradition, it is said that the Rishi vital spirits created seven square-shaped Purusha (cosmic entities, or persons) that together composed a single body, and it was from this form that Prajapati emerged once again. While art historian Wilhelm Worringer argued in 1907 that primordial art was born in the abstract line found in cave graffiti, one may assume that the artistic gesture also emerged through the composing of segments and fractions, introducing forms and geometric techniques of growing complexity. 4 In his studies of Vedic mathematics, Italian mathematician Paolo Zellini has discovered that the Agnicayana ritual was used to transmit techniques of geometric approximation and incremental growth—in other words, algorithmic techniques—comparable to the modern calculus of Leibniz and Newton. 5 Agnicayana is among the most ancient documented rituals still practiced today in India, and a primordial example of algorithmic culture.
But how can we define a ritual as ancient as the Agnicayana as algorithmic? To many, it may appear an act of cultural appropriation to read ancient cultures through the paradigm of the latest technologies. Nevertheless, claiming that abstract techniques of knowledge and artificial metalanguages belong uniquely to the modern industrial West is not only historically inaccurate but also an act and one of implicit epistemic colonialism towards cultures of other places and other times. The French mathematician Jean-Luc Chabert has noted that “algorithms have been around since the beginning of time and existed well before a special word had been coined to describe them. Algorithms are simply a set of step by step instructions, to be carried out quite mechanically, so as to achieve some desired result.” 6 Today some may see algorithms as a recent technological innovation implementing abstract mathematical principles. On the contrary, algorithms are among the most ancient and material practices, predating many human tools and all modern machines:
Algorithms are not confined to mathematics … The Babylonians used them for deciding points of law, Latin teachers used them to get the grammar right, and they have been used in all cultures for predicting the future, for deciding medical treatment, or for preparing food … We therefore speak of recipes, rules, techniques, processes, procedures, methods, etc., using the same word to apply to different situations. The Chinese, for example, use the word shu (meaning rule, process or stratagem) both for mathematics and in martial arts … In the end, the term algorithm has come to mean any process of systematic calculation, that is a process that could be carried out automatically. Today, principally because of the influence of computing, the idea of finiteness has entered into the meaning of algorithm as an essential element, distinguishing it from vaguer notions such as process, method or technique.7
Before the consolidation of mathematics and geometry, ancient civilizations were already big machines of social segmentation that marked human bodies and territories with abstractions that remained, and continue to remain, operative for millennia. Drawing also on the work of historian Lewis Mumford, Gilles Deleuze and Félix Guattari offered a list of such old techniques of abstraction and social segmentation: “tattooing, excising, incising, carving, scarifying, mutilating, encircling, and initiating.” 8 Numbers were already components of the “primitive abstract machines” of social segmentation and territorialization that would make human culture emerge: the first recorded census, for instance, took place around 3800 BCE in Mesopotamia. Logical forms that were made out of social ones, numbers materially emerged through labor and rituals, discipline and power, marking and repetition.
In the 1970s, the field of “ethnomathematics” began to foster a break from the Platonic loops of elite mathematics, revealing the historical subjects behind computation. 9 The political question at the center of the current debate on computation and the politics of algorithms is ultimately very simple, as Diane Nelson has reminded us: Who counts? 10 Who computes? Algorithms and machines do not compute for themselves; they always compute for someone else, for institutions and markets, for industries and armies.
2. What Is an Algorithm?
The term “algorithm” comes from the Latinization of the name of the Persian scholar al-Khwarizmi. His tract On the Calculation with Hindu Numerals, written in Baghdad in the ninth century, is responsible for introducing Hindu numerals to the West, along with the corresponding new techniques for calculating them, namely algorithms. In fact, the medieval Latin word “algorismus” referred to the procedures and shortcuts for carrying out the four fundamental mathematical operations—addition, subtraction, multiplication, and division—with Hindu numerals. Later, the term “algorithm” would metaphorically denote any step-by-step logical procedure and become the core of computing logic. In general, we can distinguish three stages in the history of the algorithm: in ancient times, the algorithm can be recognized in procedures and codified rituals to achieve a specific goal and transmit rules; in the Middle Ages, the algorithm was the name of a procedure to help mathematical operations; in modern times, the algorithm qua logical procedure becomes fully mechanized and automated by machines and then digital computers.
Looking at ancient practices such as the Agnicayana ritual and the Hindu rules for calculation, we can sketch a basic definition of “algorithm” that is compatible with modern computer science: (1) an algorithm is an abstract diagram that emerges from the repetition of a process, an organization of time, space, labor, and operations: it is not a rule that is invented from above but emerges from below; (2) an algorithm is the division of this process into finite steps in order to perform and control it efficiently; (3) an algorithm is a solution to a problem, an invention that bootstraps beyond the constrains of the situation: any algorithm is a trick; (4) most importantly, an algorithm is an economic process, as it must employ the least amount of resources in terms of space, time, and energy, adapting to the limits of the situation.
Today, amidst the expanding capacities of AI, there is a tendency to perceive algorithms as an application or imposition of abstract mathematical ideas upon concrete data. On the contrary, the genealogy of the algorithm shows that its form has emerged from material practices, from a mundane division of space, time, labor, and social relations. Ritual procedures, social routines, and the organization of space and time are the source of algorithms, and in this sense they existed even before the rise of complex cultural systems such as mythology, religion, and especially language. In terms of anthropogenesis, it could be said that algorithmic processes encoded into social practices and rituals were what made numbers and numerical technologies emerge, and not the other way around. Modern computation, just looking at its industrial genealogy in the workshops studied by both Charles Babbage and Karl Marx, evolved gradually from concrete towards increasingly abstract forms.
3. The Rise of Machine Learning as Computational Space
In 1957, at the Cornell Aeronautical Laboratory in Buffalo, New York, the cognitive scientist Frank Rosenblatt invented and constructed the Perceptron, the first operative artificial neural network—grandmother of all the matrices of machine learning, which at the time was a classified military secret.11 The first prototype of the Perceptron was an analogue computer composed of an input device of 20 × 20 photocells (called the “retina”) connected through wires to a layer of artificial neurons that resolved into one single output (a light bulb turning on or off, to signify 0 or 1). The “retina” of the Perceptron recorded simple shapes such as letters and triangles and passed electric signals to a multitude of neurons that would compute a result according to a threshold logic. The Perceptron was a sort of photo camera that could be taught to recognize a specific shape, i.e., to make a decision with a margin of error (making it an “intelligent” machine). The Perceptron was the first machine-learning algorithm, a basic “binary classifier” that could determine whether a pattern fell within a specific class or not (whether the input image was a triangle or not, a square or not, etc.). To achieve this, the Perceptron progressively adjusted the values of its nodes in order to resolve a large numerical input (a spatial matrix of four hundred numbers) into a simple binary output (0 or 1). The Perceptron gave the result 1 if the input image was recognized within a specific class (a triangle, for instance); otherwise it gave the result 0. Initially, a human operator was necessary to train the Perceptron to learn the correct answers (manually switching the output node to 0 or 1), hoping that the machine, on the basis of these supervised associations, would correctly recognize similar shapes in the future. The Perceptron was designed not to memorize a specific pattern but to learn how to recognize potentially any pattern.
The matrix of 20 × 20 photoreceptors in the first Perceptron was the beginning of a silent revolution in computation (which would become a hegemonic paradigm in the early twenty-first century with the advent of “Deep Learning,” a machine-learning technique). Although inspired by biological neurons, from a strictly logical point of view the Perceptron marked not a biomorphic turn in computation but a topological one; it signified the rise of the paradigm of “computational space” or “self-computing space.” This turn introduced a second spatial dimension into a paradigm of computation that until then had only a linear dimension (see the Turing machine that reads and writes 0 and 1 along a linear memory tape). This topological turn, which is the core of what people perceive today as “AI,” can be described more modestly as the passage from a paradigm of passive information to one of active information. Rather than having a visual matrix processed by a top-down algorithm (like any image edited by a graphics software program today), in the Perceptron the pixels of the visual matrix are computed in a bottom-up fashion according to their spatial disposition. The spatial relations of the visual data shape the operation of the algorithm that computes them.
Because of its spatial logic, the branch of computer science originally dedicated to neural networks was called “computational geometry.” The paradigm of computational space or self-computing space shares common roots with the studies of the principles of self-organization that were at the center of post-WWII cybernetics, such as John von Neumann’s cellular automata (1948) and Konrad Zuse’s Rechnender Raum by (1967).12 Von Neumann’s cellular automata are cluster of pixels, perceived as small cells on a grid, that change status and move according to their neighboring cells, composing geometric figures that resemble evolving forms of life. Cellular automata have been used to simulate evolution and to study complexity in biological systems, but they remain finite-state algorithms confined to a rather limited universe. Konrad Zuse (who built the first programmable computer in Berlin in 1938) attempted to extend the logic of cellular automata to physics and to the whole universe. His idea of “rechnender Raum,” or calculating space, is a universe that is composed of discrete units that behave according to the behavior of neighboring units. Alan Turing’s last essay, “The Chemical Basis of Morphogenesis” (published in 1952, two years before his death), also belongs to the tradition of self-computing structures.13 Turing considered molecules in biological systems as self-computing actors capable of explaining complex bottom-up structures, such as tentacle patterns in hydra, whorl arrangement in plants, gastrulation in embryos, dappling in animal skin, and phyllotaxis in flowers.14
Von Neumann’s cellular automata and Zuse’s computational space are intuitively easy to understand as spatial models, while Rosenblatt’s neural network displays a more complex topology that requires more attention. Indeed, neural networks employ an extremely complex combinatorial structure, which is probably what makes them the most efficient algorithms for machine learning. Neural networks are said to “solve any problem,” meaning they can approximate the function of any pattern according to the Universal Approximation theorem (given enough layers of neurons and computing resources). All systems of machine learning, including support-vector machines, Markov chains, Hopfield networks, Boltzmann machines, and convolutional neural networks, to name just a few, started as models of computational geometry. In this sense they are part of the ancient tradition of ars combinatoria.15
4. The Automation of Visual Labor
Even at the end of the twentieth century, no one would have ever thought to call a truck driver a “cognitive worker,” an intellectual. At the beginning of the twenty-first century, the use of machine learning in the development of self-driving vehicles has led to a new understanding of manual skills such as driving, revealing how the most valuable component of work, generally speaking, has never been merely manual, but also social and cognitive (as well as perceptual, an aspect of labor still waiting to be located somewhere between the manual and the cognitive). What kind of work do drivers perform? Which human task will AI come to record with its sensors, imitate with its statistical models, and replace with automation? The best way to answer this question is to look at what technology has successfully automated, as well as what it hasn’t.
The industrial project to automate driving has made clear (more so than a thousand books on political economy) that the labor of driving is a conscious activity following codified rules and spontaneous social conventions. However, if the skill of driving can be translated into an algorithm, it will be because driving has a logical and inferential structure. Driving is a logical activity just as labor is a logical activity more generally. This postulate helps to resolve the trite dispute about the separation between manual labor and intellectual labor.16 It is a political paradox that the corporate development of AI algorithms for automation has made possible to recognize in labor a cognitive component that had long been neglected by critical theory. What is the relation between labor and logic? This becomes a crucial philosophical question for the age of AI.
A self-driving vehicle automates all the micro-decisions that a driver must make on a busy road. Its artificial neural networks learn, that is imitate and copy, the human correlations between the visual perception of the road space and the mechanical actions of vehicle control (steering, accelerating, stopping) as ethical decisions taken in a matter of milliseconds when dangers arise (for the safety of persons inside and outside the vehicle). It becomes clear that the job of driving requires high cognitive skills that cannot be left to improvisation and instinct, but also that quick decision-making and problem-solving are possible thanks to habits and training that are not completely conscious. Driving remains essentially also a social activity, which follows both codified rules (with legal constraints) and spontaneous ones, including a tacit “cultural code” that any driver must subscribe to. Driving in Mumbai—it has been said many times—is not the same as driving in Oslo.
Obviously, driving summons an intense labor of perception. Much labor, in fact, appears mostly perceptive in nature, through continuous acts of decision and cognition that take place in the blink of an eye. 17 Cognition cannot be completely disentangled from a spatial logic, and often follows a spatial logic in its more abstract constructions. Both observations—that perception is logical and that cognition is spatial—are empirically proven without fanfare by autonomous driving AI algorithms that construct models to statistically infer visual space (encoded as digital video of a 3-D road scenario). Moreover, the driver that AI replaces in self-driving cars and drones is not an individual driver but a collective worker, a social brain that navigates the city and the world.18 Just looking at the corporate project of self-driving vehicles, it is clear that AI is built on collective data that encode a collective production of space, time, labor, and social relations. AI imitates, replaces, and emerges from an organized division of social space (according first to a material algorithm and not the application of mathematical formulas or analysis in the abstract).
5. The Memory and Intelligence of Space
Paul Virilio, the French philosopher of speed or “dromology,” was also a theorist of space and topology, for he knew that technology accelerates the perception of space as much as it morphs the perception of time. Interestingly, the title of Virilio’s book The Vision Machine was inspired by Rosenblatt’s Perceptron. With the classical erudition of a twentieth-century thinker, Virilio drew a sharp line between ancient techniques of memorization based on spatialization, such as the Method of Loci, and modern computer memory as a spatial matrix:
Cicero and the ancient memory-theorists believed you could consolidate natural memory with the right training. They invented a topographical system, the Method of Loci, an imagery-mnemonics which consisted of selecting a sequence of places, locations, that could easily be ordered in time and space. For example, you might imagine wandering through the house, choosing as loci various tables, a chair seen through a doorway, a windowsill, a mark on a wall. Next, the material to be remembered is coded into discreet images and each of the images is inserted in the appropriate order into the various loci. To memorize a speech, you transform the main points into concrete images and mentally “place” each of the points in order at each successive locus. When it is time to deliver the speech, all you have to do is recall the parts of the house in order.
The transformation of space, of topological coordinates and geometric proportions, into a technique of memory should be considered equal to the more recent transformation of collective space into a source of machine intelligence. At the end of the book, Virilio reflects on the status of the image in the age of “vision machines” such as the Perceptron, sounding a warning about the impending age of artificial intelligence as the “industrialisation of vision”:
“Now objects perceive me,” the painter Paul Klee wrote in his Notebooks. This rather startling assertion has recently become objective fact, the truth. After all, aren’t they talking about producing a “vision machine” in the near future, a machine that would be capable not only of recognizing the contours of shapes, but also of completely interpreting the visual field … ? Aren’t they also talking about the new technology of visionics: the possibility of achieving sightless vision whereby the video camera would be controlled by a computer? … Such technology would be used in industrial production and stock control; in military robotics, too, perhaps.
Now that they are preparing the way for the automation of perception, for the innovation of artificial vision, delegating the analysis of objective reality to a machine, it might be appropriate to have another look at the nature of the virtual image … Today it is impossible to talk about the development of the audiovisual … without pointing to the new industrialization of vision, to the growth of a veritable market in synthetic perception and all the ethical questions this entails … Don’t forget that the whole idea behind the Perceptron would be to encourage the emergence of fifth-generation “expert systems,” in other words an artificial intelligence that could be further enriched only by acquiring organs of perception.19
6. Conclusion
If we consider the ancient geometry of the Agnicayana ritual, the computational matrix of the first neural network Perceptron, and the complex navigational system of self-driving vehicles, perhaps these different spatial logics together can clarify the algorithm as an emergent form rather than a technological a priori. The Agnicayana ritual is an example of an emergent algorithm as it encodes the organization of a social and ritual space. The symbolic function of the ritual is the reconstruction of the god through mundane means; this practice of reconstruction also symbolizes the expression of the many within the One (or the “computation” of the One through the many). The social function of the ritual is to teach basic geometry skills and to construct solid buildings.20 The Agnicayana ritual is a form of algorithmic thinking that follows the logic of a primordial and straightforward computational geometry.
The Perceptron is also an emergent algorithm that encodes according to a division of space, specifically a spatial matrix of visual data. The Perceptron’s matrix of photoreceptors defines a closed field and processes an algorithm that computes data according to their spatial relation. Here too the algorithm appears as an emergent process—the codification and crystallization of a procedure, a pattern, after its repetition. All machine-learning algorithms are emergent processes, in which the repetition of similar patterns “teach” the machine and cause the pattern to emerge as a statistical distribution.21
Self-driving vehicles are an example of complex emergent algorithms since they grow from a sophisticated construction of space, namely, the road environment as social institution of traffic codes and spontaneous rules. The algorithms of self-driving vehicles, after registering these spontaneous rules and the traffic codes of a given locale, try to predict unexpected events that may happen on a busy road. In the case of self-driving vehicles, the corporate utopia of automation makes the human driver evaporate, expecting that the visual space of the road scenario alone will dictate how the map will be navigated.
The Agnicayana ritual, the Perceptron, and the AI systems of self-driving vehicles are all, in different ways, forms of self-computing space and emergent algorithms (and probably, all of the them, forms of the invisibilization of labor).
The idea of computational space or self-computing space stresses, in particular, that the algorithms of machine learning and AI are emergent systems that are based on a mundane and material division of space, time, labor, and social relations. Machine learning emerges from grids that continue ancient abstractions and rituals concerned with marking territories and bodies, counting people and goods; in this way, machine learning essentially emerges from an extended division of social labor. Despite the way it is often framed and critiqued, artificial intelligence is not really “artificial” or “alien”: in the usual mystification process of ideology, it appears to be a deus ex machina that descends to the world like in ancient theater. But this hides the fact that it actually emerges from the intelligence of this world.
What people call “AI” is actually a long historical process of crystallizing collective behavior, personal data, and individual labor into privatized algorithms that are used for the automation of complex tasks: from driving to translation, from object recognition to music composition. Just as much as the machines of the industrial age grew out of experimentation, know-how, and the labor of skilled workers, engineers, and craftsmen, the statistical models of AI grow out of the data produced by collective intelligence. Which is to say that AI emerges as an enormous imitation engine of collective intelligence. What is the relation between artificial intelligence and human intelligence? It is the social division of labor.
Matteo Pasquinelli (PhD) is Professor in Media Philosophy at the University of Arts and Design, Karlsruhe, where he coordinates the research group KIM (Künstliche Intelligenz und Medienphilosophie / Artificial Intelligence and Media Philosophy). For Verso he is preparing a monograph on the genealogy of artificial intelligence as division of labor, which is titled The Eye of the Master: Capital as Computation and Cognition.
-
Paul Virilio, La Machine de vision: essai sur les nouvelles techniques de representation (Galilée, 1988). Translated as The Vision Machine, trans. Julie Rose (Indiana University Press, 1994), 12. ↩
-
The Dutch Indologist and philosopher of language Frits Staal documented the Agnicayana ritual during an expedition in Kerala, India, in 1975. See Frits Staal, AGNI: The Vedic Ritual of the Fire Altar, vol. 1–2 (Asian Humanities Press, 1983). ↩
-
Kim Plofker, “Mathematics in India,” in The Mathematics of Egypt, Mesopotamia, China, India, and Islam, ed. Victor J. Katz (Princeton University Press, 2007). ↩
-
See Wilhelm Worringer, Abstraction and Empathy: A Contribution to the Psychology of Style (Ivan R. Dee, 1997). (Abstraktion und Einfühlung, 1907). ↩
-
See Frits Staal, “Artificial Languages Across Sciences and Civilizations,” Journal of Indian Philosophy 34, no. 1–2 (2006). ↩
-
Jean-Luc Chabert, “Introduction,” in A History of Algorithms: From the Pebble to the Microchip, ed. Jean-Luc Chabert (Springer, 1999), 1. ↩
-
Jean-Luc Chabert, “Introduction,” 1–2. ↩
-
Gilles Deleuze and Félix Guattari, Anti-Oedipus: Capitalism and Schizophrenia, trans. Robert Hurley (Viking, 1977), 145. ↩
-
See Ubiratàn D’Ambrosio, “Ethno Mathematics: Challenging Eurocentrism,” in Mathematics Education, eds. Arthur B. Powell and Marilyn Frankenstein (State University of New York Press, 1997). ↩
-
Diane M. Nelson, Who Counts?: The Mathematics of Death and Life After Genocide (Duke University Press, 2015). ↩
-
Frank Rosenblatt, “The Perceptron: A Perceiving and Recognizing Automaton,” Technical Report 85-460-1, Cornell Aeronautical Laboratory, 1957. ↩
-
John von Neumann and Arthur W. Burks, Theory of Self-Reproducing Automata (University of Illinois Press, 1966). Konrad Zuse, “Rechnender Raum,” Elektronische Datenverarbeitung, vol. 8 (1967). As book: Rechnender Raum (Friedrich Vieweg & Sohn, 1969). Translated as Calculating Space (MIT Technical Translation, 1970). ↩
-
Alan Turing, “The Chemical Basis of Morphogenesis,” Philosophical Transactions of the Royal Society of London B 237, no. 641 (1952). ↩
-
It must be noted that Marvin Minsky and Seymour Papert’s 1969 book Perceptrons (which superficially attacked the idea of neural networks and nevertheless caused the so-called first “winter of AI” by stopping all research funding into neural networks) claimed to provide “an introduction to computational geometry.” Marvin Minsky and Seymour Papert, Perceptrons: An Introduction to Computational Geometry (MIT Press, 1969). ↩
-
See the work of twelfth-century Catalan monk Ramon Llull and his rotating wheels. In the ars combinatoria, an element of computation follows a logical instruction according to its relation with other elements and not according to instructions from outside the system. See also DIA-LOGOS: Ramon Llull’s Method of Thought and Artistic Practice, eds. Amador Vega, Peter Weibel, and Siegfried Zielinski (University of Minnesota Press, 2018). ↩
-
Specifically, a logical or inferential activity does not necessarily need to be conscious or cognitive to be effective (this is a crucial point in the project of computation as the mechanization of “mental labor”). See the work of Simon Schaffer and Lorraine Daston on this point. More recently, Katherine Hayles has stressed the domain of extended nonconscious cognition in which we are all implicated. Simon Schaffer, “Babbage’s Intelligence: Calculating Engines and the Factory System,” Critical inquiry 21, no. 1 (1994). Lorraine Daston, “Calculation and the Division of Labor, 1750–1950,” Bulletin of the German Historical Institute, no. 62 (Spring 2018). Katherine Hayles, Unthought: The Power of the Cognitive Nonconscious (University of Chicago Press, 2017). ↩
-
According to both Gestalt theory and the semiotician Charles Sanders Peirce, vision always entails cognition; even a small act of perception is inferential—i.e., it has the form of an hypothesis. ↩
-
School bus drivers will never achieve the same academic glamor of airplane or drone pilots with their adventurous “cognition in the wild.” Nonetheless, we should acknowledge that their labor provides crucial insights into the ontology of AI. ↩
-
Virilio, The Vision Machine, 76. ↩
-
As Stall and Zellini have noted, among others, these skills also include the so-called Pythagorean theorem, which is helpful in the design and construction of buildings, demonstrating that it was known in ancient India (having been most likely transmitted via Mesopotamian civilizations). ↩
-
In fact, more than machine “learning,” it is data and their spatial relations “teaching.” ↩






